¡Hola! Hoy vine a dejarles algunos caramelos matemáticos fabricados por estudiantes de sexto y de séptimo.
Por ejemplo, comparto esta hermosa ilustración de la propiedad conmutativa de la suma tomada del trabajo de Jazmín:
Entre otras interesantes definiciones, esta página del glosario elaborado por Mathias nos habla de otra importantísima propiedad de la suma:
Cuando hablamos de múltiplos y divisores, hablamos de números enteros. Esto tiene que quedar bien claro. Si queremos una definición matemática, un número entero A es múltiplo de un número entero B si y solo si existe un número entero C tal que
A = B∙C
Por otro lado,
B es divisor de A
significa
A es múltiplo de B
Podemos expresar lo anterior mediante una pleca o barra vertical:
B|A
Por ejemplo, 10 es divisor de 40 porque 40 es múltiplo de 10.
Podemos escribir
10|40
También quiero compartir estos maravillosos apuntes de Maite:
¿Vieron esa descripción de la propiedad distributiva? Transcribo nuevamente las palabras de Maite: «El número que multiplica a la suma, en vez de multiplicar directamente la suma, multiplica cada uno de los números por separado». ¡Eso es tener las ideas claras!
Por otro lado, si hablamos de la propiedad conmutativa de la suma, podemos expresar la fórmula de la siguiente manera:
a + b = b + a
Les dejo también una excelente demostración propuesta por Maite sobre los números recíprocos:
El recíproco de un número a ≠ 0 es el número 1/a.
Por ejemplo, el recíproco de 4 es 1/4. Si los multiplicamos, el producto es 1.
Las definiciones elaboradas por Sofía y por Aimé promueven el pensamiento abstracto mediante el importante concepto de variable:
.jpeg) |
| ¿Se dieron cuenta de que ya habíamos estado usando variables en estos trabajos? ¿Se animan a encontrarlas en esta entrada del blog? |
En las ecuaciones usamos las variables como incógnitas. ¿Cuál es la solución de esta ecuación?
Quiero despedirme con el hermoso diccionario o glosario matemático elaborado por Charo. Es una joya de trabajo matemático:
https://drive.google.com/file/d/1C1kGnJ-8C7Gv0Afr9XnhuC1uaORImuhn/view?usp=sharing
.jpeg)
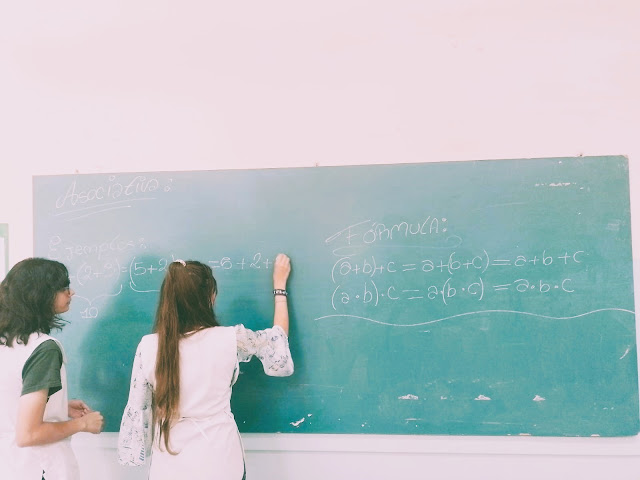
.jpeg)
.jpeg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpeg)
